Note
Go to the end to download the full example code
Why use EMD?#
The motivations behind the Empirical Mode Demposition are straightforward but sometimes get lost in a relatively complicated and technical literature. This tutorial presents a quick summary of what EMD could add to your analysis and what issues it can help to solve.
Frequency spectra of dynamic and non-sinusoidal signals#
A core challenge in signal processing is finding an intuitive representation of the frequency content of complicated and dynamic signals. The most common approach is to use methods based on the Fourier-transform - in which we represent a signal with a set of sinusoidal basis functions. This is a very powerful and flexible approach but has some short-comings when working with dynamic or non-sinusoidal signals.
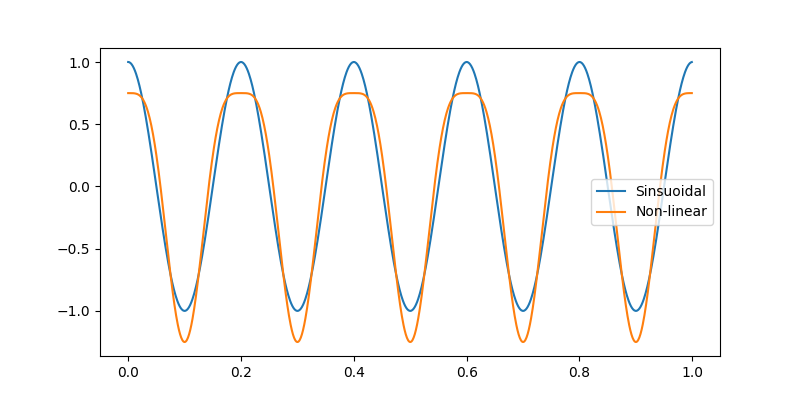
Let’s take a look at an example. Here we make two oscillatory signals - one with a sinusoidal waveform and one with a non-linearity.
import emd
import numpy as np
from scipy import signal, ndimage
import matplotlib.pyplot as plt
sample_rate = 1000
seconds = 10
num_samples = sample_rate*seconds
time_vect = np.linspace(0, seconds, num_samples)
freq = 5
# Sinusoidal signal
x = np.cos(2*np.pi*freq*time_vect)
# Non-linear signal
y = np.cos(2*np.pi*freq*time_vect) + 0.25*np.cos(2*np.pi*freq*2*time_vect-np.pi)
# Quick summary figure
plt.figure(figsize=(8, 4))
plt.plot(time_vect[:sample_rate], x[:sample_rate])
plt.plot(time_vect[:sample_rate], y[:sample_rate])
plt.legend(['Sinsuoidal', 'Non-linear'])
# sphinx_gallery_thumbnail_number = 2
<matplotlib.legend.Legend object at 0x7f0eba790d10>
We can see that our non-linear signal has a wider trough and a sharper peak than the sinusoid - many natural signals might have oscillatory features like this. Unfortunately, the Fourier transform has to use multiple components to represent this oscillation as its basis set fixed and unchanging over time.
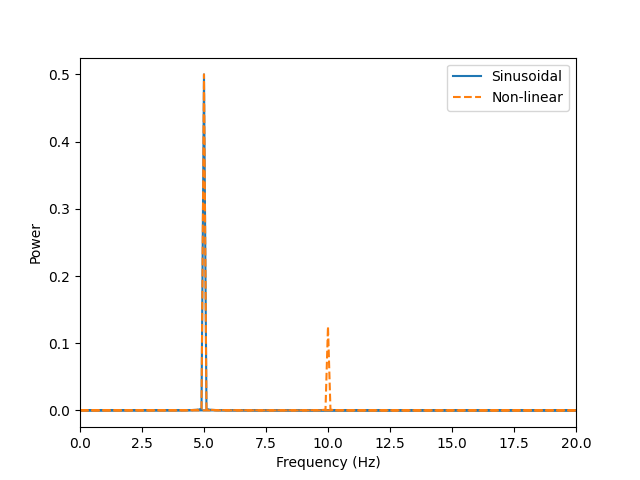
As an illustration, lets compute a fast-Fourier transform on our two signals
pxx = np.fft.fft(x) / len(x)
pyy = np.fft.fft(y) / len(x)
fft_f = np.fft.fftfreq(x.shape[0], d=time_vect[1]-time_vect[0])
plt.figure()
plt.plot(fft_f, np.abs(pxx))
plt.plot(fft_f, np.abs(pyy), '--')
plt.xlim(0, 20)
plt.legend(['Sinusoidal', 'Non-linear'])
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power')
Text(42.722222222222214, 0.5, 'Power')
Welch’s periodogram shows us that both signals have high power at 5Hz - as we would expect from our signal definition. However, the non-linear case has an additional peak at 10Hz. This arises as the Fourier transform and related methods needs to represent the non-linearity with a combination of strictly linear basis functions. We only need a signal component to represent our linear signal but the non-linear signal needs to use two. This is well illustrated in the time domain.
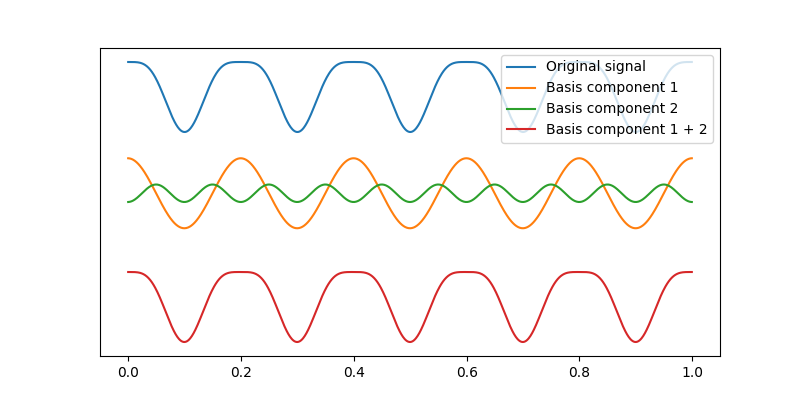
First, we can use the parameters of the Fourier transform to recompute our basis signals.
comp1_amp = 2 * np.abs(pyy[50])
comp1_phase = np.arctan2(pyy[50].imag, pyy[50].real)
comp1 = comp1_amp * np.cos(2*np.pi*5*time_vect + comp1_phase)
comp2_amp = 2 * np.abs(pyy[100])
comp2_phase = np.arctan2(pyy[100].imag, pyy[100].real)
comp2 = comp2_amp * np.cos(2*np.pi*10*time_vect + comp2_phase)
print('Component 1 amp={0} and phase={1}'.format(comp1_amp, comp1_phase))
print('Component 2 amp={0} and phase={1}'.format(comp2_amp, comp2_phase))
Component 1 amp=0.9999422181181443 and phase=0.015707963267943763
Component 2 amp=0.2500380507261862 and phase=-3.1101767270538976
The values recovered from the fourier transform are very close to the simulated values from the start. We see that the first component has an amplitude very close to 1 and a phase close to zero, whilst the second component has an amplitude close to 0.25 and a phase close to -pi.
plt.figure(figsize=(8, 4), frameon=False)
plt.yticks([])
plt.plot(time_vect[:sample_rate], y[:sample_rate] + 3)
plt.plot(time_vect[:sample_rate], comp1[:sample_rate])
plt.plot(time_vect[:sample_rate], comp2[:sample_rate])
plt.plot(time_vect[:sample_rate], comp1[:sample_rate] + comp2[:sample_rate] - 3)
plt.legend(['Original signal', 'Basis component 1', 'Basis component 2', 'Basis component 1 + 2'])
<matplotlib.legend.Legend object at 0x7f0eba63e650>
The top signal in blue is our simulated signal, the orange and green signals are the two components identified by the Fourier transform coefficients which sum together to create the bottom signal in red.
It turns out that any signal can be represented by the summation of sets of simple sinusoids - even extremely non-linear or disjoint signals like triangular waves. This is a very powerful tool, but the need to include multiple high frequency components, known as harmonics, can create interpretation issues. In a complex or noisy signal, it might not be clear whether a peak in a power spectrum represents a harmonic of a low frequency signal or a stand-alone high frequency signal. The problem gets worse if we have several oscillations which are all creating separate harmonics. These signals may be untangled using more complicated analysis of the interactions between different Fourier components but these can get very complicated.
Instantaneous Frequency#
The Empirical Mode Decomposition offers a different perspective on this problem. Instead of representing dynamic signals with combinations of static basis functions, the EMD looks to isolate a small number of temporally adaptive basis functions and derive dynamics in frequency and amplitude directly from them.
These adaptive basis functions are called Intrinsic Mode Functions (IMFs) and are isolated from the data using the ‘sift’ algorithm. This is a time-domain algorithm which doesn’t require a Fourier transform to separate out different signals.
IMFs are defined by several features. They must be locally-symmetric around zero and contain the same number of extrema as zero-crossings (or differ by no more than 1). The ‘sift’ is a numerical algorithm for isolating signal components with exactly these features. Any residual after the sift is a non-oscillatory trend component.
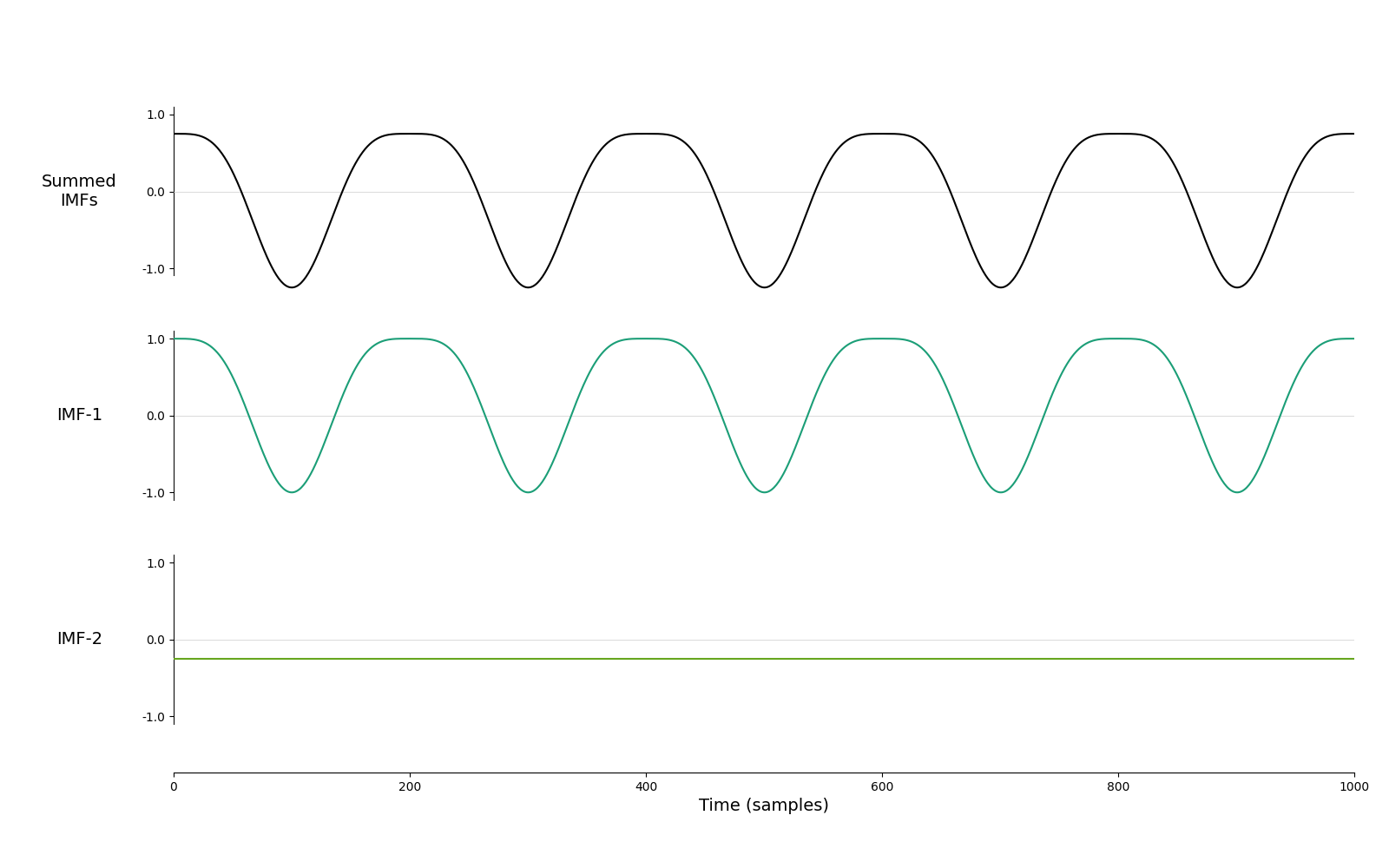
Lets run a sift on our non-linear signal and plot the results.
imf = emd.sift.sift(y)
emd.plotting.plot_imfs(imf[:sample_rate, :])
<Axes: xlabel='Time (samples)'>
The sift has identified two components, the first contains the oscillatory signal with its non-sinusoidal shape intact whilst the second contains a constant mean-term.
We can compute the instantaneous amplitude, frequency and phase of our IMF using the Hilbert transform. This is a function which creates an ‘analytic’ form of a signal that is extremely useful for extracting dynamic information from a signal. Critically, the result of a Hilbert transform is only valid for signals with very specific features. The definition of the sift ensures that each resulting IMF does meet these criteria (or at least be very close).
This means that we can use the Hilbert transform to estimate instantaneous frequencies directly from our IMFs. We don’t need to use the Fourier transform for this and so can avoid adding harmonic components into our results.
Here, we compute the Hilbert transform from our IMFs
IP, IF, IA = emd.spectra.frequency_transform(imf, sample_rate, 'hilbert')
…and plot up the resulting instantaneous frequency.
plt.figure(figsize=(10, 6))
plt.subplots_adjust(hspace=0.4)
plt.subplot(211)
plt.plot(time_vect[:sample_rate], imf[:sample_rate, 0])
plt.title('IMF-1')
plt.subplot(212)
plt.plot(time_vect[:sample_rate], IF[:sample_rate, 0])
plt.title('IMF-1 Instantaneous Frequency')
plt.ylabel('Frequency (Hz)')

Text(100.84722222222221, 0.5, 'Frequency (Hz)')
This dynamic representation of frequency is able to adapt to the changing waveform shape and describe the non-sinusoidal shape as a single smoothly varying component rather than as two separate, static components.
We can compute a power spectrum using these principles called the Hilbert-Huang transform
freq_range = (0.1, 20, 32)
hht_f, spec = emd.spectra.hilberthuang(IF, IA, freq_range, scaling='density')
plt.figure()
plt.plot(fft_f, np.abs(pyy))
plt.plot(hht_f, spec)
plt.legend(['Fourier Transform', 'Hilbert-Huang Transform'], frameon=False)
plt.xlim(0, 20)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power')
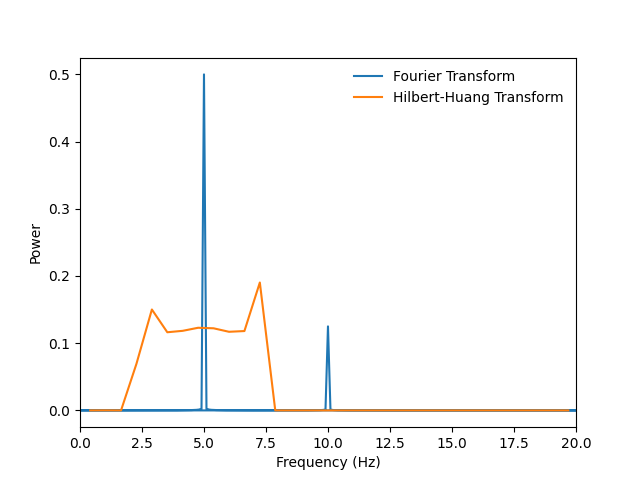
Text(42.722222222222214, 0.5, 'Power')
The Hilbert-Huang transform gives a summary of the dynamic spectral content of the signal. It represents our non-linear signal as a distribution of frequencies around 5Hz without adding an additional signal component.
Time-resolution#
Finally, the instantaneous frequency and amplitude from the Hilbert transform allow us to see very rapid dynamics in oscillatory signals. Fourier methods are able to see dynamic changes by applying the transform in a sliding window but the choice of window size places an important constraint on the time-frequency resolution of the transform. Longer windows have greater frequency resolution as they are able to use a larger number of Fourier basis components - however these longer windows necessarily lead to worse time resolution.
In contrast, the instantaneous frequency stats naturally vary over time, so no window choice is required. Let’s take a closer look with a dynamic simulation.
# Create a signal with a dynamic oscillation
z = emd.simulate.ar_oscillator(25, sample_rate, seconds, r=0.975)[:, 0]
First we compute the sift, frequency transform and the Hilbert-Huang spectrum
imf = emd.sift.sift(z)
IP, IF, IA = emd.spectra.frequency_transform(imf, sample_rate, 'hilbert')
freq_range = (0.1, 50, 48)
hht_f, hht = emd.spectra.hilberthuang(IF, IA, freq_range, mode='amplitude', sum_time=False)
hht = ndimage.gaussian_filter(hht, 1)
Next, we compute a short-time Fourier-transform. The nperseg variable
controls the window-length and time-frequency resolution. Higher values will
lead to greater precision in frequency and worse precision in time.
nperseg = 2048
ftf, ftt, ftZ = signal.stft(z, nperseg=nperseg, fs=sample_rate, noverlap=nperseg-1)
plt.figure(figsize=(8, 10))
plt.subplot(311)
plt.plot(time_vect, z)
plt.xlim(1, 9)
plt.title('Signal')
plt.subplot(312)
plt.pcolormesh(ftt, ftf, np.abs(ftZ), cmap='hot_r')
plt.ylim(0, 50)
plt.xlim(1, 9)
plt.title('Short-Time Fourier-Transform')
plt.ylabel('Frequency (Hz)')
plt.subplot(313)
plt.pcolormesh(time_vect, hht_f, hht, cmap='hot_r')
plt.ylim(0, 50)
plt.title('Hilbert-Huang Transform')
plt.xlim(1, 9)
plt.xlabel('Time (seconds)')
plt.ylabel('Frequency (Hz)')

Text(67.09722222222221, 0.5, 'Frequency (Hz)')
Changes in oscillatory power are visible in both transforms but are noticeably smoother in the STFT compared to the HHT. The blur in the STFT is due to the windowing that we have applied, we can try to reduce this window size to increase the temporal resolution of our transform
nperseg = 512
ftf, ftt, ftZ = signal.stft(z, nperseg=nperseg, fs=sample_rate, noverlap=nperseg-1)
Now we plot the two transforms together for another comparison.
plt.figure(figsize=(8, 10))
plt.subplot(311)
plt.plot(time_vect, z)
plt.xlim(1, 9)
plt.title('Signal')
plt.subplot(312)
plt.pcolormesh(ftt, ftf, np.abs(ftZ), cmap='hot_r')
plt.ylim(0, 50)
plt.xlim(1, 9)
plt.title('Short-Time Fourier-Transform')
plt.ylabel('Frequency (Hz)')
plt.subplot(313)
plt.pcolormesh(time_vect, hht_f, hht, cmap='hot_r')
plt.ylim(0, 50)
plt.title('Hilbert-Huang Transform')
plt.xlim(1, 9)
plt.xlabel('Time (seconds)')
plt.ylabel('Frequency (Hz)')
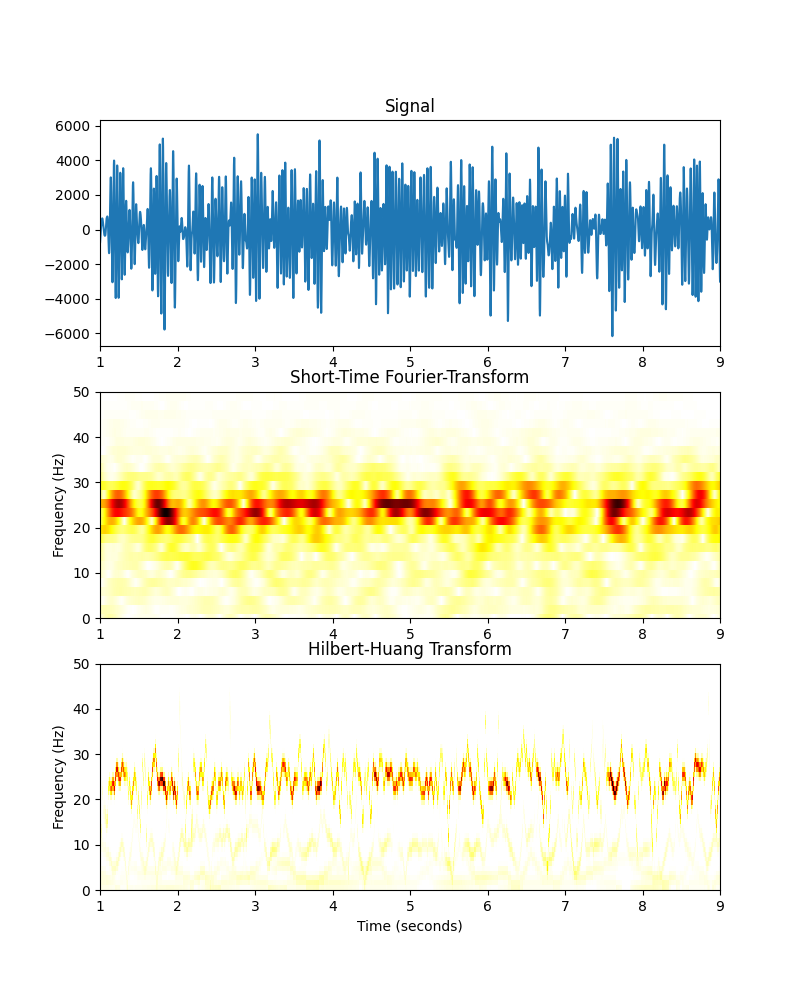
Text(67.09722222222221, 0.5, 'Frequency (Hz)')
Shortening the window-size in the STFT has reduced the temporal blur but increased the blur in the frequency dimension. The HHT produces a sharper image in both dimensions.
The remaining tutorials go into all of the above analysis in much more detail and try to introduce the motivations and concepts behind EMD alongside a range of practical examples. We also introduce some problems with the EMD and how to recognise & reduce them - there is no free-lunch in signal processing!
Total running time of the script: (0 minutes 7.973 seconds)
